Answer: The correct option is (A) Angle W is greater than angle Y.
Step-by-step explanation: Given that the measures of the three sides of a triangle XYZ are as follows:
XY = 10 units,
WY = 14 units,
WX = 5 units.
We are to select the correct statements regarding the angles of ΔXYZ.
Writing the lengths of the sides in ascending order, we have
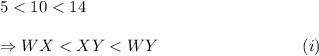
Since the angle opposite to a smaller side of a triangle is smaller, so from inequality (i), we get
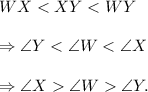
Option (A) is "Angle W is greater than angle Y".
This option is correct, because we have ∠W > ∠Y.
Option (B) is "Angle Y is the largest angle".
This is incorrect because ∠X is the largest angle.
Option (C) is "Angle X is smaller than angle W"
This is incorrect because ∠X is the largest.
Option (D) is "Angle W is the smallest angle".
This is incorrect because ∠Y is the smallest.
Thus, (A) is the correct option.