Question

The centers for disease control and prevention reports 25% baby boys 6 to 8 months in the US weigh more than 20 pounds a sample of babies 16 is studied what is the probability that fewer than three weigh more than 20 pounds?

Answer 1

P(x < 3) = 0.1971

Step-by-step explanation:

To calculate the probability that x babies weigh more than 20 pounds, we will use the binomial distribution, so it can be calculated as:

`\begin{gathered} P(x)=nCx\cdot p^x\cdot(1-p)^(n-x) \\ Where\text{ nCx=}(n!)/(x!(n-x)!) \\ \\ With\text{ n = size of sample} \\ p=\text{ probability of success \lparen the baby weight more than 20 pounds\rparen} \end{gathered}`

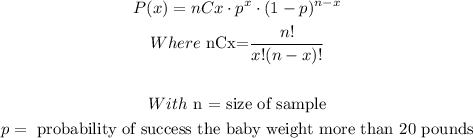
So, replacing n = 16 and p = 0.25, we get that the probability is equal to

P(x) = 16Cx (0.25)^x (1 - 0.25)^(16 - x)

`P(x)=16Cx\cdot0.25^x\cdot(1-0.25)^(16-x)`

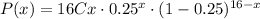
Now, the probability that fewer than three weights more than 20 pounds are equal to

`\begin{gathered} P(x<3)=P(0)+P(1)+P(2) \\ Where \\ P(0)=16C0\cdot0.25^0\cdot(1-0.25)^(16-0)=0.01 \\ P(1)=16C1\cdot0.25^1\cdot(1-0.25)^(16-1)=0.0535 \\ P(2)=16C2\cdot0.25^2\cdot(1-0.25)^(16-2)=0.1336 \end{gathered}`

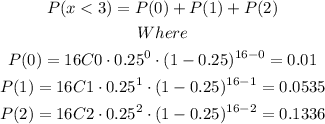
Then

P(x < 3) = 0.01 + 0.0535 + 0.1336

P(x < 3) = 0.1971

Therefore, the answer is

P(x < 3) = 0.1971