a)
To determine which transformation from the function:
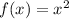
we are making we need to remember that:
From the table we conclude that to get function M we need to do the following trasnformations:
• Translate function f 14.979 units to the left.
,
• Vertical compression with a factor of 0.0037
The sketch of the graph is shown below:
b)
To rewrite the function so that t=0 represents the year 2000 we need to translate the function M 10 units to the left, that is we add 10 to the variable t, then we have:
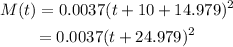
Therefore the function we need here is:
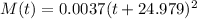
c)
For the year 2014 fourteen years have passed from 2000; plugging 14 in the model in part b we have:
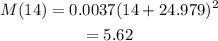
Therefore in 2014 the debt is 5.62 trillions of dollars.