Question

Consider the equation (x^m)3=(x^13)^5*(x^-8)^-5

the value of m is
a.15
b.28
c.35
d.70

Answer 1

The answer will be 35

Answer 2

Option C is correct.

The value of m for the given equation is, 35

Explanation:

Given an equation:
`(x^m)^3=(x^(13))^5*(x^(-8))^(-5)`

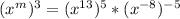
To multiply the power of pwer, multiply the exponents on both sides of an equation:

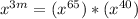`x^(3m)=(x^(65))*(x^(40))` ...[1]

Using Property: When multiplying powers with the same base, then add the exponents.

Use the above property on RHS in equation [1];

Since the base are same i.e, x ; we can add the exponents.

`x^(3m)=x^(65+40)` or

`x^(3m)=x^(105)`

Using:
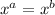`x^a=x^b` , then a=b.

Therefore, 3m=105.

Divide 3 on both sides of an equation:

`(3m)/(3) =(105)/(3)`

Simplify:

m=35

Therefore, the valur of m is, 35.