Before the first straw is drawn, there are three short straws and
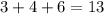
straws in all. Thus, the probability of drawing a short straw first is
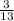
.
After a short straw is drawn, there are two short straws and twelve total straws, a probability of

.
Thus, the probability of both of these events occurring is
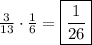
.