Question

The house was bought for $125,000 in 1990, the overage rate is 7.85%, what year will the purchase of the house be worth 3 times the purchase price?

Answer 1

Answer: 2005

Explanation:

Exponential function to determine the value of item after t years,

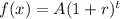`f(x)=A(1+r)^t` , where r= rate of growth, A=Initial value.

As per given , A = 7.85% = 0.0785

A = $125,000

Substitute all values in function, we get

`f(x)=125000(1+0.785)^t`

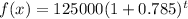
When f(x)= 3A , then

`3A=A(1.0785)^t\\\\\Rightarrow\ 3=(1.0785)^t`

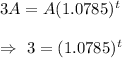
Taking tog on both sides , we get

`\ln 3=t\ln 1.0785\\\\\Rightarrow\ t=(\ln 3)/(\ln 1.0785)\\\\\Rightarrow t=(1.09861228867)/(0.0755711868471)\approx15`

The year will be 1990+15= 2005

Hence, the required year = 2005