We can see that the quadrilateral is located in the points:
M(1, -2)
X(3, -3)
E(-2, -4)
J(-2, -3)
After this we can see that the vector represents the following rule:
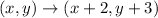
So, we calculate the new coordinates M'X'E'J':
M'(3, 1)
x'(5, 0)
E'(0, -1)
J'(0, 0)
So, the first translation is:
After this, we reflect across the y-axis to obtain M''X''E''J'', that is following the rule:
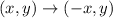
So, we find the new points:
M''(-3, 1)
X''(-5, 0)
E''(0, -1) = E'(0, -1)
J''(0, 0) = J'(0, 0)
Finally, the y-axis reflection is:
And that is the first and final positions of the points.
***Here all of the transformations in one image: