Question

You deposit $3000 in an account that pays 3.5% interest compounded once a year. Your friend deposits $2500 in an account that pays 4.8% interest compounded monthly.a. Who will have more money in their account after one year? How much more? b. Who will have more money in their account after five years? How much more? c. Who will have more money in their account after 20 years? How much more?

Answer 1

Formula for compound interest:

`F=P(1+r)^n^{}`

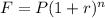
Where

F is future value

P is initial amount

r is rate of interest [in decimal]

n is number of years [or time period]

Now,

a)

Your money in 1 year will be:

`\begin{gathered} F=3000(1+0.035)^1 \\ F=3105 \end{gathered}`

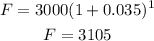
Money for your friend in 1 year:

compounded monthly, so there will be 12 compounding in a year

n = 12

also, yearly interet is 4.8%, monthly will be 4.8/12 = 0.4%

0.4% means 0.4/100 = 0.004

So, we get:

`\begin{gathered} F=2500(1+0.004)^(12) \\ F=2622.675 \\ F=2622.68 \end{gathered}`

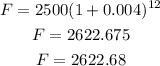
You will have more money after 1 year.

By 3105 - 2622.68 = 482.32 dollars more.

b)

After 5 years, you will have:

`\begin{gathered} F=3000(1+0.035)^5 \\ F=3563.06 \end{gathered}`

After 5 years, your friend will have:

r stays the same at 0.4% per month

n gets changed to 12 * 5 = 60 months

So, your friend will have:

`\begin{gathered} F=2500(1.004)^(60) \\ F=3176.60 \end{gathered}`

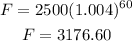
After 5 years, you will have more money.

By 3563.06 - 3176.60 = 386.46 dollars more

c)

After 20 years, you will have:

`\begin{gathered} F=3000(1+0.035)^(20) \\ F=5969.37 \end{gathered}`

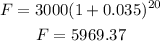
After 5 years, your friend will have:

r stays the same at 0.4% per month

n gets changed to 12 * 20 = 240 months

So, your friend will have:

`\begin{gathered} F=2500(1.004)^(240) \\ F=6516.75 \end{gathered}`

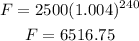
After 5 years, your friend will have more money.

By 6516.75 - 5969.37 = 547.38 dollars more