Formula for compound interest:
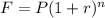
Where
F is future value
P is initial amount
r is rate of interest [in decimal]
n is number of years [or time period]
Now,
a)
Your money in 1 year will be:
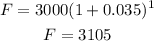
Money for your friend in 1 year:
compounded monthly, so there will be 12 compounding in a year
n = 12
also, yearly interet is 4.8%, monthly will be 4.8/12 = 0.4%
0.4% means 0.4/100 = 0.004
So, we get:
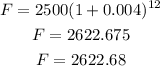
You will have more money after 1 year.
By 3105 - 2622.68 = 482.32 dollars more.
b)
After 5 years, you will have:
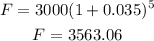
After 5 years, your friend will have:
r stays the same at 0.4% per month
n gets changed to 12 * 5 = 60 months
So, your friend will have:
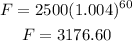
After 5 years, you will have more money.
By 3563.06 - 3176.60 = 386.46 dollars more
c)
After 20 years, you will have:
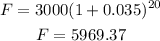
After 5 years, your friend will have:
r stays the same at 0.4% per month
n gets changed to 12 * 20 = 240 months
So, your friend will have:
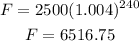
After 5 years, your friend will have more money.
By 6516.75 - 5969.37 = 547.38 dollars more