Question

Solve for X, (with steps please)
0.46=0.527-[0.0562/2 * log(0.1+x/1.5-x)]

Answer 1

Rearrange the equation:


`(0.0562)/(2) * log( (0.1+x)/(1.5 - x)) = 0.527 - 0.46 = 0.067`

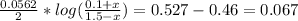
Isolate the log on its own


`log ((0.1 + x)/(1.5 - x)) = (0.067*2)/(0.0562) = 2.42 (2dp)`

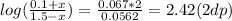
To get rid of the log you must do 10^2.42


`(0.1 +x)/(1.5-x) = 10^(2.42) = 242.29 (2dp)`

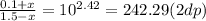
Then multiply both sides by (1.5 - x)


`0.1 +x = 242.29(1.5-x)`


`0.1 + x = 363.44 - 242.29x`

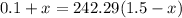
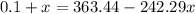
Solve normally


`image`

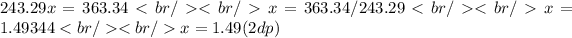
Hope that helps. Please send me a message if there's patchy bits. Also I'm sure you'll figure this out, but just in case, anywhere I've put down a 2dp shows that I've rounded the number to 2 decimal places. It becomes a pain to deal with otherwise.