We write an inequality:
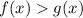
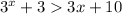
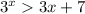
This equation cannot be solved using trivial methods found in high-school classes, so we resort to graphical examination.
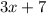
is a linear function while

is an exponential one (with limit zero as

approaches
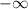
). We see that

at approximately
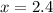
and

.
Indeed, using a computer algebra system such as the ones on modern TI calculators and on many internet sites gives equality at
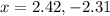
. By observing our graph, we see that
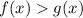
when
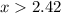
or

.