Question

A component in a music system has a life expectancy of 2,400 hours with a standard deviation of 300 hours. If an average person listens to music for 1,000 hours in a year, the probability that the component lasts for more than 3 years is %. NextReset

Answer 1

2.3 % is the answer for the question

Answer 2

2.228%

Explanation:

Average life = 2400 hours

So,
`\mu = 2400`

`\sigma = 300`

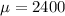
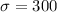
An average person listens to music for 1,000 hours in a year

So, An average person listens to music in 3 years=
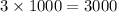`3 * 1000 = 3000` hours

Now we are supposed to find the probability that the component lasts for more than 3 years

`z=(x-\mu)/(\sigma)`

`z=(3000-2400)/(300)`

`z=2`

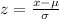
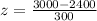
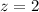
So,P(z<3000 hours or 3 years)=P(z<2)=0.9772

So,P(z>2)=1-0.9772=0.0228 or
`0.0228 *d 100 = 2.228 \%`

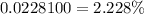
Hence the probability that the component lasts for more than 3 years is 2.228%