Question

Need the answer I don't know how to work it.

Answer 1

`\bf (y-k)=a(x-h)^2\qquad \begin{cases} vertex\ (h,k)\\ vertex\ (-4,2) \end{cases}\\\\\\ y-2=a(x-(-4))^2 \implies y=a(x+4)^2+2`

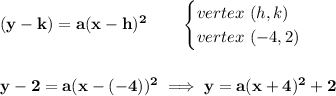
so.. what is the coefficient "a"?
well
now, we know, another point on the graph, besides the vertex, we know a y-intercept, that is, 0, -30, that simply means when x = 0, y = -30


`\bf y=a(x+4)^2+2\qquad (0,-30)\implies -30=a(0+4)^2+2 \\\\\\ -30-2=a4^2\implies \cfrac{-32}{16}=a\implies -2=a \\\\\\ thus\implies y=-2(x+4)^2+2`

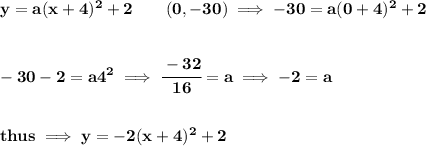
now, getting the x-intercepts, is just the zeros, or solution to the quadratic


`\bf y=-2(x+4)^2+2\impliedby \textit{setting y to 0} \\\\\\ 0=-2(x+4)^2+2\implies -2=-2(x+4)^2\implies \cfrac{-2}{-2}=(x+4)^2 \\\\\\ 1=(x+4)^2\implies \pm√(1)=x+4\implies \pm 1-4 = x\to \begin{cases} (-3\ ,\ 0)\\ (-5\ ,\ 0) \end{cases}`

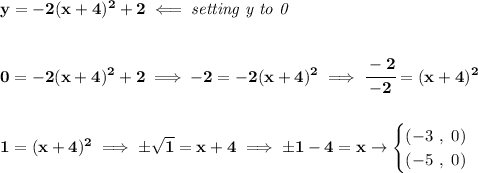
notice, "y" is 0 on both cases, because, is an x-intercept, or a zero, and when the graph touches the x-axis, "y" is zero