Question

Luke has a job at a garden center where he is paid $12.00 per hour, but also has a side job coaching basketball where he makes $18.75 per hour. He must make at least $795 per week to cover his expenses but cannot work more than 55 hours per week. If x represents the hours he works at the garden center and y represents the hours he coaches basketball, do the following. Write a system of inequalities that models this situation.

Answer 1

`\begin{gathered} 12x+18.75y\ge795 \\ x+y\leq55 \end{gathered}`

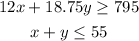
Step-by-step explanation

Step 1

Let

x represents the hours he works at the garden center

y represents the hours he coaches basketball

so, the earnings from the garden center are=12x

and the earnings from the basketabll are=18.75y

the toal earned would be

`\text{total =12x+18.75 y}`

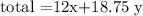
He must make at least $795 per week to cover his expenses ,so

`\begin{gathered} \text{total }\ge795 \\ \text{replacing} \\ 12x+18.75y\ge795\rightarrow Inequality\text{ (1)} \end{gathered}`

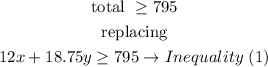
and,he cannot work more than 55 hours per week,so

`x+y\leq55\rightarrow Inequality\text{ (2)}`

I hope this helps you