Question

A volleyball reaches its maximum height of 13 feet, 3 seconds after its served. Which of the following quadratics could model the height of the vollyball over time after it is served. Select all that apply.

A: f(x)=2x^2+12x+5

B: f(x)=-2x^2+12x-5

C: f(x)=-2x^2-12x+5

D: f(x)=-2(x-3)^2+13

E: f(x)=-2(x+3)^2+13

Answer 1

B and D wl/wkejbgvejbfvejbf

Answer 2

Answer with explanation:

It is given that, a volleyball reaches its maximum height of 13 feet, 3 seconds after its served.

→If,we take height of volleyball along Y axis,and time along X axis,then Coordinates of Vertex can be represented as , (3,13).Because trajectory or path of Volleyball will be In the Shape of Parabola.

So,equation of parabola will be in the form of :

→
`y-13=-4 a(x-3)^2`

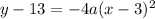
--------------------------------(1)

Negative sign indicates that ,the parabola is opening Downwards.

Or,

→If,we take height of volleyball along X axis,and time along Y axis,then Coordinates of Vertex can be represented as , (13,3).Because trajectory or path of Volleyball will be In the Shape of Parabola.

So, equation of parabola will be in the form of :

→
`y-3=- 4 a(x-13)^2`

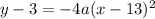
--------------------------------(1)

Negative sign indicates that ,the parabola is opening Downwards.

→→→If you will look at the options Carefully ,and try to match with options

or just check that , points (3,13) and (13,3) satisfies which equations,you will find that , Option B and Option D, that is , equation , B: f(x)=-2 x²+12 x-5 and D: f(x)=-2(x-3)²+13 ,passes through, (3,13).