Answer:
C. 0.36
Explanation:
We have been given that owners in the area claim that there is a 45% chance that the land has oil. Jason buys a kit that claims to have an 80% accuracy rate of indicating oil in the soil. We are asked to find the probability that the land has oil and the test predicts it.

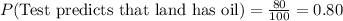
Since both events are independent, so probability that land has oil and test predicts will be product of probabilities both events.
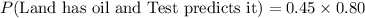
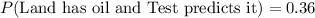
Therefore, the probability that the land has oil and the test predicts it would be 0.36 and option C is the correct choice.