Question

Sketch the graph of the following function. f:R→R, f(x)=−(x−1)2+4.(a) Indicate zeros of the function.(b) Discuss the behaviour of f(x) for x → −∞ and x → ∞.(c) Let P = (xP , yP ) be the point where the f intersects the y-axis. Determine the coordinates of P.

Answer 1

`f(x)=-(x-1)^2+4`

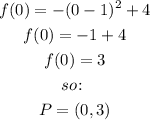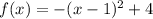
(a)

This is a parabola which has a vertex located at (1,4). Since the leading coefficient is negative, it opens downwards. So:

(b)

As we can see:

`\begin{gathered} \lim _(x\to-\infty)f(x)=-\infty \\ \lim _(x\to\infty)f(x)=-\infty \end{gathered}`

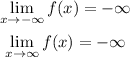
In both cases, the function tends to -∞.

(c)

We can find these coordinates evaluating the function for x = 0, so:

`\begin{gathered} f(0)=-(0-1)^2+4 \\ f(0)=-1+4 \\ f(0)=3 \\ so\colon \\ P=(0,3) \end{gathered}`