Question

Let f(x)=(x+4)^2−3.

Let g(x)=(x+4)^2+6.



Which statement describes the graph of g(x) with respect to the graph of f(x)?



It is compressed vertically by a factor of −4.

It is translated right 9 units.

It is translated up 9 units.

It is stretched horizontally by a factor of −4.
PLEASE HELP THANK YOU

Answer 1

its translated upwards by 6 - (-3) = 9 units
third choice is correct

Answer 2

f(x) is translated up 9 units to get g(x)

C is correct.

Explanation:

Given:

`f(x)=(x+4)^2-3`

`g(x)=(x+4)^2+6`

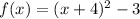
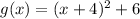
We need to compare the graph of g(x) with respect to graph of f(x)

So, we will subtract g(x)-f(x)

`g(x)-f(x)=(x+4)^2+6-(x+4)^2+3`

Simplify the expression

`g(x)-f(x)=6+3`

`g(x)=f(x)+9`

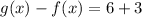
Here, g(x) will get by addition of 9 to f(x).

It is vertical shift. Here Addition of 9 so, f(x) will shift 9 unit up to get g(x)

Hence, f(x) is translated up 9 units to get g(x)