Question

Solve the equation 2^(2x+1)+8=17×2^x.

Answer 1

oooh, looks fun

ok
erm
we might want to know some properties

`(x^m)(x^n)=x^(m+n)`

`(a^b)^c=a^(bc)`
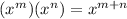
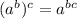
if
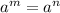
`a^m=a^n` where a=a, then assume m=n


`2^(2x+1)=(2^(2x))(2^1)`
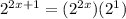
so

`(2^(2x))(2)+8=17(2^x)`

`(2^(2x))(2)+2^3=17(2^x)`

`(2^x)^2(2)+2^3=17(2^x)`
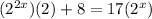
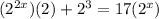
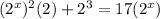
minus 17*2^x both sides

`(2^x)^2(2)+2^3-17(2^x)=0`
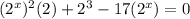
use u subsitution, u=2ˣ

`(u)^2(2)+2^3-17(u)=0`
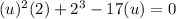
solve
`2u^2+8-17u=0`
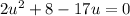
or

`2u^2-17u+8=0`
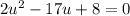
ac method
2 times 8=16
what 2 number multiply to get -17 and add to get 16
-16 and -1
2u²-1u-16u+8=0
(2u²-1u)+(-16u+8)=0
u(2u-1)+(-8)(2u-1)=0
(u-8)(2u-1)+0
u-8=0
u=8

2u-1=0
2u=1
u=1/2

now
u=2ˣ

8=2ˣ

`2^3=2^x`
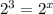
3=x

and

`(1)/(2)=2^x`

`2^(-1)=2^x`
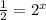
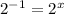
-1=x

x=-1 and 3
neat problem