Answer:
The option which gives the formula for a new function h created by shrinking g by a factor of 2 along the y-axis is:

Explanation:
We are given a parent function which is a exponential function as:
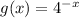
and the shrinking of a function along the y-axis means that there is a vertical shrink.
Now, it is given that the function g is vertically compressed by a factor of 2.
This means that the transformed function is given by:
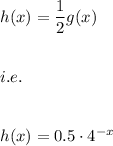
Also, by the graph we could observe that at x=0 the value of x is compressed when the function was divided by 2.