Answer: The answer is (B) y ≤ –2x + 3 .
Step-by-step explanation: We are to select the correct linear inequality that could represent the table of values given in the question.
If (x, y) = (-4, -1), then
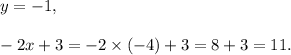
So, y < -2x + 3.
If (x, y) = (-2, 4), then
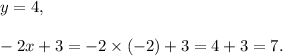
So, y < -2x + 3.
If (x, y) = (3, -3), then
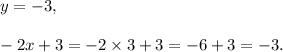
So, y = -2x + 3.
If (x, y) = (3, -4), then
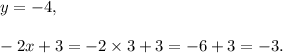
So, y < -2x + 3.
Therefore, we have y is either less than or equal to (-2x + 3).
Thus, y ≤ –2x + 3 and (B) is the correct option.