Question

A 200 gallon tank initially contains 100 gallons of water with 20 pounds of salt. A salt solution with 1/4 pound of salt per gallon is added to the tank at 4 gal/min, and the resulting mixture is drained out at 2 gal/min. Find the quantity of salt in the tank as it’s about to overflow.

Answer 1

The volume of the solution in the tank is


`V(t)=100+(4-2)t=100+2t`

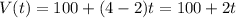
and so the solution will overflow when
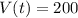
`V(t)=200`. This happens at
`t=50`.

Now the rate of change of the amount of salt in the tank at time
`t`,
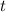
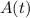
`A(t)`, is described by


`(\mathrm dA)/(\mathrm dt)=\left(\frac14\text{ lb/gal}\right)\left(4\text{ gal/min}\right)-\left((A(t))/(100+2t)\text{ lb/gal}\right)\left(2\text{ gal/min}\right)`

`A'+\frac A{50+t}=1`

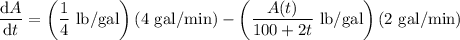
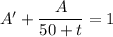
which is linear in
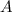
`A`. Multiplying both sides by
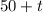
`50+t`, we have


`(50+t)A'+A=50+t`

`\bigg((50+t)A\bigg)'=50+t`

`(50+t)A=\displaystyle\int(50+t)\,\mathrm dt=50t+\frac12t^2+C`

`A=(100t+t^2)/(100+2t)+\frac C{50+t}`

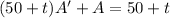
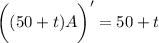
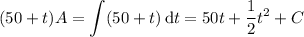
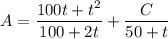
There are 20 lbs of salt in the tank at the start, so
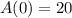
`A(0)=20` and we get that


`20=0+\frac C{50}\implies C=1000`

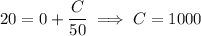
so that the amount of salt in the tank is given by the function


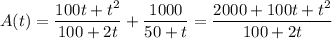
`A(t)=(100t+t^2)/(100+2t)+(1000)/(50+t)=(2000+100t+t^2)/(100+2t)`

At
`t=50`, the tank contains


`A(50)=(2000+100(50)+50^2)/(100+2(50))=\frac{95}2`

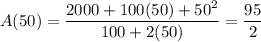
pounds of salt.