Question

You are asked to do a study of shelters for abused and battered women to determine the necessary capacity in your city to provide housing for most of these women. After recording data for a whole year, you find that the mean number of women in shelters each night is 250, with a standard deviation of 75. Fortunately, the distribution of the number of women in the shelters each night is normal, so you can answer the following question posed by the city. How many beds will they have 95% of the time. Please round to a whole number.

Answer 1

We know that

• The mean is 250.

,

• The standard deviation is 75.

,

• The distribution is normal.

To find the number of beds they will have 95% of the time, first, we have to find the z-score with the following formula.

`z=(x-\mu)/(\sigma)`

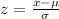
Where,

`\begin{gathered} \mu=250 \\ \sigma=75 \end{gathered}`

We have to find the probability of

`P(z<(x-\mu)/(\sigma))=0.05`

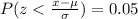
Since the complement part of 95% is 5% which is equal to 0.05.

Using the z-core table below, we find that the z-score assigned to 0.050 is -1.6.

Then, we have the equation and solve for x.

`\begin{gathered} (x-250)/(75)=-1.6 \\ x-250=-1.6\cdot75 \\ x-250=-120 \\ x=-120+250=130 \end{gathered}`

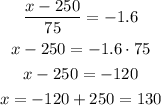
Therefore, they have 130 beds 95% of the time.