Question

Consider the function f(x) = 1/x on the interval [1, 10] Find the average or mean slope of the function on this interval.

Answer 1

We will have the following:

First, we determine the equation for the slope, that is:

`f(x)=(1)/(x)\Rightarrow f^(\prime)(x)=-(1)/(x^2)`

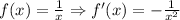
Now, to determine the average slope we examine the slopes at the edges:

`\begin{gathered} f^(\prime)(1)=-(1)/(1^2)\Rightarrow f^(\prime)(1)=-1 \\ \\ and \\ \\ f^(\prime)(10)=-(1)/((10)^2)\Rightarrow f^(\prime)(10)=-(1)/(100) \end{gathered}`

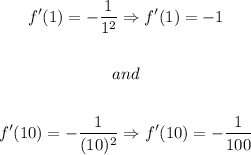
So, the average slope will be given by:

`\begin{gathered} m_a=((-(1)/(100))+(-1))/(2)\Rightarrow m_a=-(101)/(200) \\ \\ \Rightarrow m_a=-0.505 \end{gathered}`

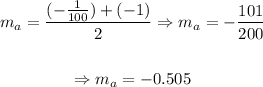
So, the average slope in that interval is -0.505.

Now, we determine the exact point where the slope is that, that is:

`\begin{gathered} -0.505=-(1)/(x^2)\Rightarrow x^2=(1)/(0.505) \\ \\ \Rightarrow x=\sqrt{(1)/(0.505)}\Rightarrow x=1.407195089... \\ \\ \Rightarrow x\approx1.4 \end{gathered}`

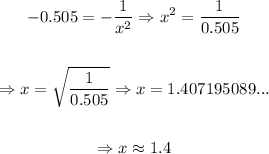
So, the exact point is sqrt( 1 / 0.505), that is approximately 1.4.