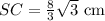Since the base of the pyramid is a triangle with a side length of 4 cm
That means the base is an equilateral triangle of sides 4 cm
The height of the equilateral triangle is
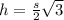
h is the height
s is the side
Since the side is 4 cm, then
s = 4
Substitute it in the rule above to find h
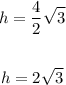
(a)
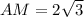
Since the rule of the area of a triangle is
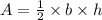
b is the base
h is the height
Since the base is 4, then
b = 4
Substitute the values of b and h in the rule of the area to find it

(b)
The area of the base is
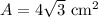
Since the altitude of the pyramid is 4 cm
We will use the Pythagoras theorem to find the side SC
From the triangle above we will use the height of the pyramid OS and a part of the height of the base = 2/3 h to find the side SC

Take a square root for both sides
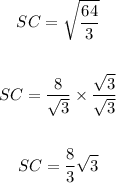
(c)
The length of the side edge SC is