Question

Carbon-14 decays at a constant rate, so it can be used to determine the age of fossils. In particular, if the original amount of Carbon-14 present is A0, then A(t) = A0e-kt can be used find the amount of amount of Carbon-14 remaining after t years. Given that the half-life of Carbon-14 is 5,730 years, what is the value of the decay constant k to 5 decimal places?

Answer 1

k = ln (.5) / Half-Life
k = -.693147 / 5,730

k = -0.0001209681

Answer 2

Value of the decay constant k = 0.00012

Explanation:

Formula to determine the age of the fossils by C-14 decay is given as

`A_(t)=A_(0)e^(-kt)`

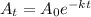
where A(t) = C-14 remaining after t years

A0 = original amount of C-14

K = decay constant

t = time taken for decay

Now we have to calculate the value of constant k when half life of C-14 is given as 5730 years.

Since half life has been given therefore final amount after 5730 years will be A/2 and initial amount will be A.

Now the equation becomes as

`(A)/(2)=Ae^((-k)(5730))`

`(1)/(2)=e^(-5730k)`

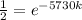
Now by taking natural log on both the sides

`ln((1)/(2))=ln(e^(-5730k))`

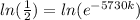
ln 1 - ln2 = -5730k (since lne = 1)

0 - ln2 = -5730k

`0.63915=5730k`

k = 0.00012

Therefore k = 0.00012 is the answer.