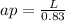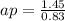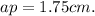Answer:
1.75 cm.
Explanation:
To find the apothem we are going to use two formulas: the formula of area (because the only data given is the area) and the formula to find the apothem.
Formula of area = 4*L*ap where L is the length of one side of the octagon and ap is the length of the apothem.
Formula of apothem =
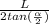 , where L is the
, where L is the
length of one side of the octagon and
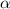 is the central angle (I show you where is that angle in the picture below). You can find the principal angle dividing the meausre of the full turn by the amount of sides:
is the central angle (I show you where is that angle in the picture below). You can find the principal angle dividing the meausre of the full turn by the amount of sides:
 . Then, we have that
. Then, we have that
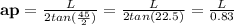 .
.
So, we have now the to formulas:
 , that is
, that is
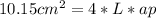 and
and
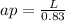 . Let's replace the second formula in the first formula to have only one unknown value:
. Let's replace the second formula in the first formula to have only one unknown value:
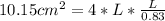
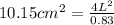
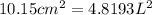
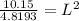
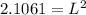
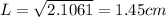 .
.
Finally, let's find the apothem replacing L in the apothem formula: