Question

Find the hypotenuse of each isosceles right triangle when the legs are of the given measure.

Answer 1

This is a 45/45/90 triangle, meaning that one angle is 90 degrees and the two legs both are 45 degrees. So, we can come to the conclusion that both of the legs are the same, which is the 3 radical two.

The hypotenuse in this type of triangle is twice as big, so we would multiply 3 radical 2 by radical 2. That gives us 6 for an answer.

So, the hypotenuse equals 6.
If you need help multiplying radicals let me know and I can explain :)

Answer 2

Answer: The required length of the hypotenuse is 6 units.

Step-by-step explanation: We are given to find the length of the hypotenuse of each isosceles right-triangle when the legs are of the following measure :

`l=3\sqrt2~\textup{units}.`

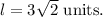
As shown in the attached figure below, triangle ABC is an isosceles right-angled triangle, where

`m\angle B=90^\circ,~~AB=BC=l=3\sqrt2~\textup{units}.`

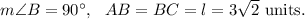
We are to find the length of the hypotenuse AC.

Using Pythagoras theorem in right-angled triangle ABC, we have

`AC^2=AB^2+BC^2\\\\\Rightarrow AC^2=l^2+l^2\\\\\Rightarrow AC^2=(3\sqrt2)^2+(3\sqrt2)^2\\\\\rightarrow AC^2=18+18\\\\\Rightarrow AC^2=36\\\\\Rightarrow AC=6.`

Thus, the required length of the hypotenuse is 6 units.