Answer:
a = 4.95 cm
Explanation:
The area formula for a regular polygon is A = 1/2 ap, where a is the apothem and p is the perimeter. We have neither the apothem nor the perimeter, so we will have to do some fancy algebra to solve for the apothem.
An octagon is made up of 8 congruent triangles, each with a vertex angle of 45 degrees (360 divided by 8 is 45). So that means that each base angle is 67.5 degrees. If we extract one of these triangles and then drop an altitude, we have then half of that triangle with a (the apothem) as the height of the triangle and 1/2s as the base. Since we split the triangle in half, we have only 1/2 the base of the whole triangle. The side measuring a is across from the angle measuring 67.5, and the base of 1/2s is adjacent to the angle, so we can use the tangent ratio to put the perimeter in terms of the apothem. Keep in mind that the p in our formula is 8s:
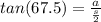
The tan(67.5) has a value of 2.414213562, and the right side becomes 2a/s:
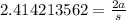 so
so
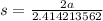 and
and
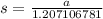
Subbing the value of s in and using the fact that the area was given, our formula becomes, in terms of a:
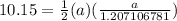 which simplifies to
which simplifies to
 which simplifies to
which simplifies to
24.50426766 = a² so
a = 4.95