Question

Mel slides down waterslide A, and Victor slides down waterslide B. After 2 seconds, Mel was 50 feet in the air, and after 5 seconds, she was 35 feet in the air. After 1 second, Victor was 60 feet in the air, and after 4 seconds, he was 50 feet in the air. Who was descending at a faster average rate?

Write ordered pairs relating Mel’s and Victor’s positions at a given time (i.e., (time, height)).

Mel: (2, ) and (5, )

Victor: (1, ) and (, )

Answer 1

Mel (2, 50) and (5, 35)
Victor (1, 60) and (4, 50)

Answer 2

We have two systems in this problem, namely:

System A. Mel slides down water slide A. So, let's name
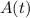`A(t)` the position of Mel at a given time, that represents her height. In this way, we know that:

`t=2s \rightarrow A(2)=50ft \\ \\ t=5s \rightarrow A(5)=35ft`

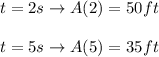
System B. Victor slides down water slide B. So, let's name
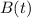`B(t)` the position of Victor at a given time, that represents his height. Thus, we know that:

`t=1s \rightarrow B(1)=60ft \\ \\ t=4s \rightarrow B(4)=50ft`

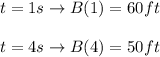
So, we have the following questions:

1. Who was descending at a faster average rate?

For a nonlinear graph whose slope changes at each point, the average rate of change between any two points
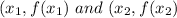`(x_(1),f(x_(1)) \ and \ (x_(2),f(x_(2))` is given by:

`ARC=(f(x_(2))-f(x_(1)))/(x_(2)-x_(1))`

`For \ Mel: \\ \\ ARC=(35-50)/(5-2)=-5ft/s \\ \\ \\ For \ Victor: \\ \\ ARC=(50-60)/(4-1)=-3.33ft/s`

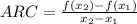
So Mel was descending at a faster average rate.

2. Ordered pairs relating Mel’s positions at a given time.

We can write these ordered pairs as follows:

`\boxed{Mel: (2, 50) \ and \ (5, 35)}`

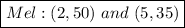
That is, after 2 seconds, Mel was 50 feet in the air, and after 5 seconds, she was 35 feet in the air.

3. Ordered pairs relating Victor’s positions at a given time.

We can write these ordered pairs as follows:

`\boxed{Victor: (1,60) \ and \ (4,50)}`

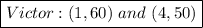
That is, after 1 second Victor was 60 feet in the air, and after 4 seconds, he was 50 feet in the air.