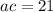Question

The diagonals of rhombus abcd intersect at point

e. the area of abcd is 168 .if ed = 8 inches, find ac.

Answer 1

The area of a rhombus is 1/2 times the lengths of the diagonals

A = (1/2)(AC)(BD)

Since the diagonals bisect each other, and ed = 8, BD must be 16. Substituting in this for BD and the given area (168) we get the following:

168 = (1/2)(AC)16
168 = 8(AC)
21 = AC

Answer 2

ac= 21

Explanation:

Rhombus is a parallelogram in which diagonals bisect each other .

Given: Area of rhombus is 168 .

The diagonals of rhombus abcd intersect at point e. It's diagonals are ac and bd . We know that diagonals of rhombus bisect each other ,so, bd=2de . So,
`bd=2(8)=16` .

Also, area of rhombus is
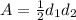`A=(1)/(2)d_1d_2` where
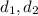`d_1,d_2` are the diagonals of rhombus .

As area of rhombus is 168 , we get ,

`168=(1)/(2)d_1d_2`

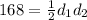
Let
`d_1=bd=16`

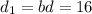
So, we get ,

`168=(1)/(2)d_1d_2\\168=(1)/(2)\left ( 16 \right )d_2\\168=8d_2\\d_2=(168)/(8)\\=21`

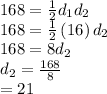
Therefore,
`ac=21`