Question

What is the missing reason in step 3?

ANSWER CHOICES :
1) triangle angle sum theorem
2) SAS congruency theorem
3) SSS congruency theorem
4) CPCTC

Answer 1

The answer is #3, SSS Congruency theorem

Answer 2

Option 3 is correct

SSS congruency theorem

Explanation:

In ΔADC and ΔCBA

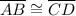`\overline{AB} \cong \overline {CD}` [Side] [Given]

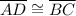`\overline{AD} \cong \overline {BC}` [Side] [Given]

Reflexive property states that any value is equal to itself

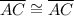`\overline{AC} \cong \overline {AC}` [Side] [Reflexive Property]

SSS -Side-Side-Side postulates states that that if three sides of one triangle are congruent to three sides of another triangle, then these two triangles are congruent.

Therefore,

ΔADC
`\cong` ΔCBA [By SSS]

By CPCT (Corresponding Part of Congruent Triangle]

`\angle DAC \cong \angle BCA` and

`\angle ACD \cong \angle CAB`

Alternate interior angle states that a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal.

therefore, by definition of alternate interior angle ;

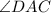`\angle DAC` and
`\angle BCA` are alternate interior angle

also,
`\angle ACD` and
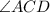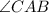`\angle CAB` are alternate interior angle

By converse of the alternate interior angle theorem states that if two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.

therefore, we have

`\overline{AB} || \overline{CD}` ;

`\overline{AD} || \overline{BC}`

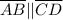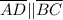
Then,by the definition of parallelogram that a four sided flat shape with straight sides where opposite sides are parallel.

⇒ABCD is parallelogram hence proved!