Question

the demand equation for a certain product is given by P=132-0.08x where P is the unit price (in dollars ) of the product and x is the number of units produced the total revenue obtained by producing and selling x units is given by R=xp determine prices p that would yield a revenue of 8830 dollarsLowest price=___highest price=_____

Answer 1

P= 132 - 0.08x

R = xP

R = x ( 132 - 0.08x)

R = 132x - 0.08x^2

8830 = 132x - 0.08 x^2

0.08x^2 - 132x + 8830 = 0 (transposing all ters to the lefthand side of the eq.)

x^2 - 1650x + 110375 = 0 (dividing all terms of the eq by 0.08)

Solve the equation using quadratic formula.

where a = 1 b = -1650 and c = 110375

Quadratic Formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-(-1650)\pm\sqrt[]{(-1650)^2-4(1)(110375)}}{2(1)}`
`x=\frac{1650\pm\sqrt[]{2722500-441500}}{2}=\frac{1650\pm\sqrt[]{2281000}}{2}=(1650\pm1510.30)/(2)`

`x=(1650\pm1510.30)/(2)\Rightarrow(1650+1510.30)/(2)\Rightarrow(1650-1510.30)/(2)`
`x_1=(1650+1510.30)/(2)=1580.15`
`x_2=(1650-1510.30)/(2)=69.85_{}`

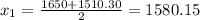
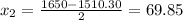
x1 and x2 are the number of units sold at the lowest and highest price respectively that yields a profit of $8830

Now, we wil solve for P= 132 - 0.08x for x1 and x2

(x1 will give us the lowest price since it has the higher number of units than x2, and it follows that x2 will give us the highest price)

Lowest Price, P = 132 - 0.08x1 = 132 - 0.08 (1580.15) = $ 5.588

Highest Price, P = 132 - 0.08x2 = 132 - 0.08 (69.85 ) = $ 126.412