$19.47
1) Examining the graph, we can write two coordinate pairs the x-coordinate for the minutes and the y-coordinate for the cost. So we have (54, 17.04) and (86, 19.92) so we can find from that the rule of this function. Let's find the slope of it:
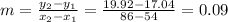
Note that the slope shows how steep is the line of that function.
2) Let's find the linear coefficient, where the graph intercepts the y-axis.
Writing the slope-intercept form:
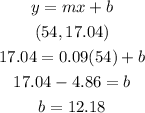
So the rule of this function is:
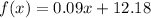
3) Now we can find out the answer, by plugging into that equation x=81

Thus, the monthly cost for 81 minutes is $19.47