Question

A certain radioisotope has a half-life of 8.0 hours; how much of a 192 g sample of this radioisotope would decay after a full day?

Answer 1

167.9895 grams sample of this radioisotope would decay after a full day.

Step-by-step explanation:

`N=N_o* e^(-\lambda t)`

`\lambda =(0.693)/(t_(1/2))`

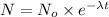
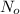`N_o` = initial amount of radioisotope

N = Amount of radioisotope left after time t.

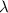`\lambda` = Decay Constant

`t_(1/2)` = Half life of the radioisotope

We have:

`N_o=192 g`

`t_(1/2)=8.0 hours`

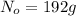
t = 1 day = 24 hour

`\lambda =(0.693)/(8.0 hour)=0.086625 hour^(-1)`

`N=192 g* e^{-0.086625 hour^(-1)* 24 hours}`

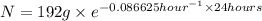
N = 24.0105 g

24.0105 grams of radioisotope will remain after 1 whole day.

Amount of radioisotope decayed =
`N_o-N=192 g- 24.0105 g=167.9895 g`

167.9895 grams sample of this radioisotope would decay after a full day.