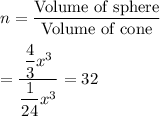Question

A cone’s height and its radius are each equal to half the radius of a sphere. How many of these cones would it take to equal the volume of the sphere? A)16 B)24 C)32 D)48

Answer 1

C) 32

Explanation:

Answer 2

Answer: 32

Explanation:

Given: A cone’s height and its radius are each equal to half the radius of a sphere.

Let x be the radius of the sphere, then the radius of cone =x/2

and height of the cone = x/2

The volume of sphere is given by :

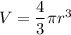`V=(4)/(3)\pi r^3`, where r is the radius of sphere.

`\Rightarrow\ V=(4)/(3)x^3`

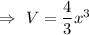
The volume of cone is given by :

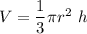`V=(1)/(3)\pi r^2\ h`, where r is the radius and h is height of the cone .

`\Rightarrow\ V=(1)/(3)\pi ((x)/(2))^2((x)/(2))\\\\\Rightarrow\ V=(1)/(24)x^3`

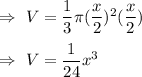
The number of cones would it take to equal the volume of the sphere is given by :-

`n=\frac{\text{Volume of sphere}}{\text{Volume of cone}}\\\\=((4)/(3)x^3)/((1)/(24)x^3)=32`