Question

A farmer stacked hay bales. The length and width of each hay bale are shown in the picture. The volume of each hay bale is 10 2/3 cubic feet. The farmer stacked 8 haynales on top of one another. What is the height, in feet, of the stacked hay bales. PLEASE HELP!!

Answer 1

you do the reverse volume function to find out the height of one.
10.6/4 equals 2.6
2.6/1.3 equals 2.
2 times 8 is 16.
The hay bales are 16 feet tall

Answer 2

16 ft.

Explanation:

We have been given that the length of each hay bale is 4 ft and the width of each hay bales is
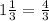`1(1)/(3)=(4)/(3)` ft. We are also given that the volume of each hay bale is
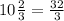`10(2)/(3)=(32)/(3)` cubic ft.

We will use volume of cuboid formula to find the height of each bale.

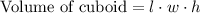`\text{Volume of cuboid}=l\cdot w\cdot h`, where,

l = Length of cuboid,

w = Width of cuboid,

h = Height of cuboid.

Upon substituting our given values in above formula we will get,

`(32)/(3)=4\cdot (4)/(3)\cdot h`

`(32)/(3)=(16)/(3)\cdot h`

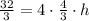
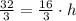
Upon multiplying both sides of our equation by
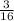`(3)/(16)` we will get,

`(32)/(3)* (3)/(16)=(16)/(3)* (3)/(16)\cdot h`

`2=h`

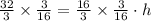
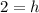
Since we are asked to find the height of 8 hay bales stacked on each other, so we will multiply height of each hay bale by 8.

`\text{Height of 8 hay bales}=8* 2=16`

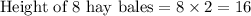
Therefore, the height of the stacked hay bales is 16 feet.