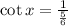Question

Find the values of the six trigonometric functions of an angle in standard position if the point with coordinates (6,-5) lies on its terminal side.

Answer 1

This is an angle in the 4th quadrant
tan 0f this angle = opp/adj = -5/6
cotangent = 1/tan = -6/5

length of hypotenuse = sqrt (6^2 + (-5)^2 ) = sqrt 61

so sine = -5/sqrt61
and cosec = 1/sin = -aqrt61/5

and cosine = 6/sqrt61
and secant = 1 / cos = sqrt61 /6

Answer 2

Given : The point with coordinates (6,-5) lies on its terminal side.

To find : The values of the six trigonometric functions of an angle in standard position

Solution :

The coordinates (6,-5) lies in the 4 quadrant.

Refer the attached figure.

where x=6 is the base

y= -5 is the perpendicular

Applying Pythagoras theorem,

`H^2=P^2+B^2`

`H^2=(-5)^2+6^2`

`H^2=25+36`

`H=√(61)`

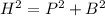
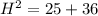
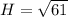
Now, finding trigonometric function

Note - In fourth quadrant only cos and sec is positive rest are negative.

1 )
`\sin x= - (P)/(H)`

`\sin x= - (-5)/(√(61))`

`\sin x= (5)/(√(61))`

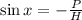
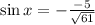
2)
`\csc x=(1)/(\sin x)`

`\csc x=(1)/((5)/(√(61)))`

`\csc x=(√(61))/(5)`

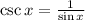
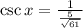
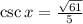
3)
`\cos x= (B)/(H)`

`\cos x=(6)/(√(61))`

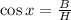
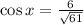
4)
`\sec x=(1)/(\cos x)`

`\sec x=(1)/((6)/(√(61)))`

`\sec x=(√(61))/(6)`

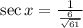
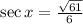
5)
`\tan x= - (P)/(B)`

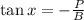
`\tan x= - (-5)/(6)`

`\tan x= (5)/(6)`

6)
`\cot x=(1)/(\tan x)`

`\cot x=(1)/((5)/(6))`

`\cot x=(6)/(5)`