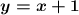Question

What is the slope-intercept form(-2,-1),(-4,-3)

Answer 1

To solve the exercise, we can first find the slope of the line that passes through the given points using the following formula:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

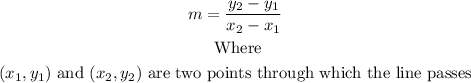
So, in this case, we have:

`\begin{gathered} (x_1,y_1)=(-2,-1) \\ (x_2,y_2)=(-4,-3) \\ m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ m=(-3-(-1))/(-4-(-2)) \\ m=(-3+1)/(-4+2) \\ m=(-2)/(-2) \\ m=1 \end{gathered}`

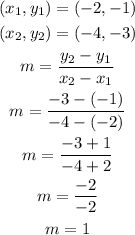
Now, we can use the point-slope formula, and we solve for y:

`y-y_1=m(x-x_1)\Rightarrow\text{ Point-slope formula}`
`\begin{gathered} y-(-1)=1(x-(-2)) \\ y+1=x+2 \\ \text{ Subtract 1 from both sides of the equation} \\ y+1-1=x+2-1 \\ y=x+1 \end{gathered}`

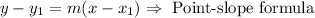
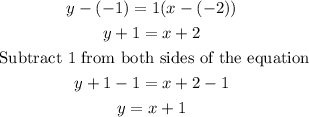
Therefore, the equation of the line that passes through the points (-2, -1) and (-4, -3) in its slope-intercept form is:

`$$\boldsymbol{y=x+1}$$`