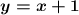To solve the exercise, we can first find the slope of the line that passes through the given points using the following formula:
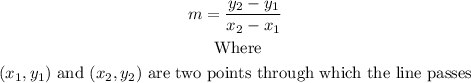
So, in this case, we have:
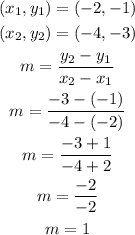
Now, we can use the point-slope formula, and we solve for y:
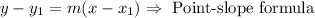
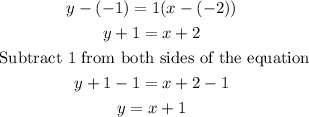
Therefore, the equation of the line that passes through the points (-2, -1) and (-4, -3) in its slope-intercept form is: