Answer:
(x+4)^2 = -8(y+3)
Explanation:
Given that the focus of a parabola is (-4, -5), and its directrix is y = -1.
We know that a parabola is a curve which has equal distance from focus and the directrix
If (x,y) be any point on the parabola, then

Square both the sides
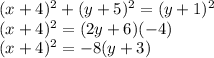
Thus std form of the parabola is
(x+4)^2 = -8(y+3)