Question

In an instant lottery, your chances of winning are 0.2. suppose you play the lottery 5 times and outcomes are independent. using the binomial probability distribution, the probability that you win at most once is

Answer 1

0.73728

Explanation:

Your chances of winning are p=0.2, then your chances of not winning are q=1-0.2=0.8.

The probability that you win at most once is equal to the sum of probabilities that you will win once or do not win at all.

Find the probability that you will win once

`P_1=C^5_1p^1q^(5-1)=(5!)/(1!(5-1)!)\cdot (0.2)^1\cdot (0.8)^4=(5!)/(4!)\cdot 0.2\cdot 0.4096=5\cdot 0.08192=0.4096`

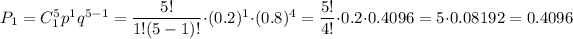
Find the probability that you will not win

`P_0=C^5_0p^0q^(5-0)=(5!)/(0!(5-0)!)\cdot (0.2)^0\cdot (0.8)^5=(5!)/(5!)\cdot (0.8)^5=1\cdot 0.32768=0.32768`

Thus, the probability that you win at most once is

`P=P_1+P_0=0.4096+0.32768=0.73728`