Question

Use trigonometry identities algebraic methods and inverse trigonometric functions as necessary to solve the following trigonometric equation on the interval round your answer to four decimal places if necessary if there is no solution indicate no solution

Answer 1

Given the equation:

`8\cos (2x)-36\cos (x)+28=0`

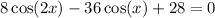
Let's solve the equation over the interval [0, 2π).

Let's simplify the equation:

Apply the double angle identity

`8(2\cos ^2x-1)-36_{}\cos x+28=0`

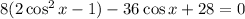
Apply distributive property:

`\begin{gathered} 8(2\cos ^2x)+8(-1)-36\cos x+28=0 \\ \\ 16\cos ^2x-8-36\cos x+28=0 \\ \\ 16\cos ^2x-36\cos x+28-8=0 \\ \\ 16\cos ^2x-36\cos x+20=0 \end{gathered}`

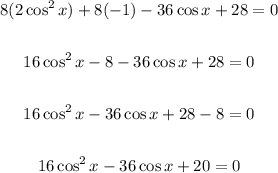
Factorize:

`4(4\cos ^2x-9\cos x+5)=0`
`\begin{gathered} 4(\cos ^2x(-4-5)\cos x+5)=0 \\ \\ 4(\cos x(\cos x-1)-5(\cos x-1))=0 \\ \\ 4(\cos x-1)(4\cos x-5)=0 \end{gathered}`

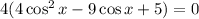
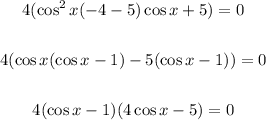
Take the individual factors and equate to zero:

• cos x-1 = 0

,

• 4cosx- - 5 = 0

Solve each factor for x:

`\begin{gathered} \cos x-1=0 \\ \\ \cos x=1 \\ \\ x=\cos ^(-1)1 \\ \\ x=0 \end{gathered}`

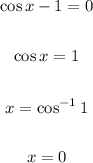
Subtract the reference angle from 2π

`\begin{gathered} x=2\pi-0 \\ \\ x=2\pi \\ \\ \text{ find the period:} \\ x=(2\pi)/(1)=2\pi \\ \\ x=2\pi\text{ n, 2}\pi+2\pi\text{ n } \\ \text{For any interger} \end{gathered}`

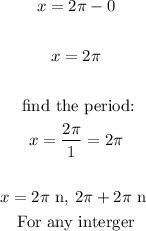
Second factor:

`\begin{gathered} 4\cos x-5=0 \\ \\ 4\cos x=5 \\ \\ \cos x=(5)/(4) \\ \end{gathered}`

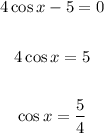
• The range for cosine is -1 ≤x ≤ 1.

Since cos x is not in the range, there is no solution,.

Input 0 for n in 2πn and solve:

`2\pi\text{ n = }2\pi(0)=0`

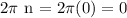
Therefore, the interval contains:

x = 0

ANSWER:

x = 0