Answer:
The exponential equation is in form of x= log base 10 of 27, all over log base 10 of 3
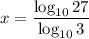
B is correct
Explanation:
Given: Exponential equation 3ˣ = 27
We need to write in logarithmic form with base 10
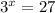
First we will apply log both sides with base 10
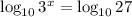
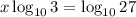
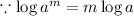
Now, we will divide by
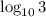 both sides
both sides
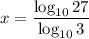
Hence, The exponential equation is in form of x= log base 10 of 27, all over log base 10 of 3