The Solution:
Let the speed without the tailwind (wind) be represented with x.
And let the speed of the wind be represented with y.
The Speed without wind:
Given that a jet can only fly 2408 miles in 4 hours.
By formula,
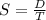
Where,
D = distance = 2408 miles
T = time = 4 hours
S = (x - y) miles/hour
Substituting these values in the formula, we get
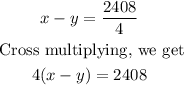
Dividing both sides by 4, we get
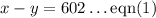
Similarly,
The Speed with the wind:
Given that the jet fly 2704 miles in 4 hours with a tailwind.
Again, the formula:
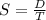
Where,
D = distance = 2704 miles
T = time = 4 hours
S = (x + y) miles/hour
Substituting these values in the formula, we get
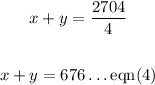
Solving both equations as simultaneous equations.
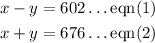
By the elimination method, we shall add their corresponding terms together in order to eliminate y.
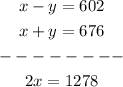
Dividing both sides by 2, we get
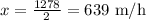
Thus, the speed of the jet in still air (without wind) is 639 miles/hour.
To solve for y:
We shall substitute 639 for x in eqn(2)
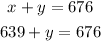
Collecting the like terms, we get
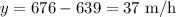
Therefore, the speed of the wind is 37 miles/hour.