Question

A private jet can fly 2704 miles in four hours with a tailwind, but only 2408 miles in four hours with a headwind.What is the speed of the jet in still air?What is the speed of the wind?

Answer 1

The Solution:

Let the speed without the tailwind (wind) be represented with x.

And let the speed of the wind be represented with y.

The Speed without wind:

Given that a jet can only fly 2408 miles in 4 hours.

By formula,

`S=(D)/(T)`

Where,

D = distance = 2408 miles

T = time = 4 hours

S = (x - y) miles/hour

Substituting these values in the formula, we get

`\begin{gathered} x-y=(2408)/(4) \\ \text{ Cross multiplying, we get} \\ 4(x-y)=2408 \end{gathered}`

Dividing both sides by 4, we get

`x-y=602\ldots\text{eqn}(1)`

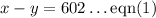
Similarly,

The Speed with the wind:

Given that the jet fly 2704 miles in 4 hours with a tailwind.

Again, the formula:

`S=(D)/(T)`

Where,

D = distance = 2704 miles

T = time = 4 hours

S = (x + y) miles/hour

Substituting these values in the formula, we get

`\begin{gathered} x+y=(2704)/(4) \\ \\ x+y=676\ldots\text{eqn}(4) \end{gathered}`

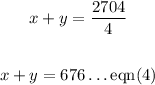
Solving both equations as simultaneous equations.

`\begin{gathered} x-y=602\ldots\text{eqn}(1) \\ x+y=676\ldots\text{eqn}(2) \end{gathered}`

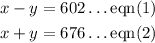
By the elimination method, we shall add their corresponding terms together in order to eliminate y.

`\begin{gathered} x-y=602 \\ x+y=676 \\ -------- \\ 2x=1278 \end{gathered}`

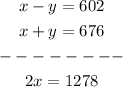
Dividing both sides by 2, we get

`x=(1278)/(2)=639\text{ m/h}`

Thus, the speed of the jet in still air (without wind) is 639 miles/hour.

To solve for y:

We shall substitute 639 for x in eqn(2)

`\begin{gathered} x+y=676 \\ 639+y=676 \end{gathered}`

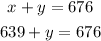
Collecting the like terms, we get

`y=676-639=37\text{ m/h}`

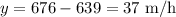
Therefore, the speed of the wind is 37 miles/hour.