Question

Q1 :Let f(x)=2x^2−8

The quadratic function g(x) is f(x) translated 2 units down

What is the equation for g(x)

Q2 Let f(x)=
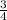
`(3)/(4)`x2−1.

The function g(x) is a vertical stretch of f(x) by a factor of 8.

What is the equation of g(x)?

Q3 The graph of the function g(x) is a transformation of the parent function f(x)=x2 .

Which equation describes the function g?
(refer to picture attached)
A. g(x)=x2+2 ​
B. g(x)=(x−2)2
C. g(x)=(x+2)2 ​
D. g(x)=x2−2

Answer 1

Q1 : g(x) = 2x^2 - 10
Q2 : g(x) = 6x^2 - 1 (8*.75)
Q3 : A.

Answer 2

Q1)
`g(x)=2x^2-10`

Q2)
`g(x)=6x^2-1`

Q3) A.
`g(x)=x^2+2`

Explanation:

Q1) being
`f(x)=2x^2-8` and g(x) is the same function but translated 2 units down, that is:

`g(x)=f(x)-2\\g(x)=2x^2-8-2\\g(x)=2x^2-10`

Q2)
`f(x)=(3)/(4)x^2-1` and f(x) has a vertical stretch, the vertical strech is given by multiplying the X factor for the stretch:

`g(x)=8*(3)/(4)x^2-1\\\\g(x)=6x^2-1`

Q3) Looking at the graph we can notice that thhe function g(x) is the same fuction f(x) but it has been displaced 2 units up, so:

`g(x)=f(x)+2\\g(x)=x^2+2`

The correct answer is A.