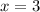Answer:
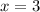
Explanation:
we have
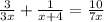
The domain of the function is all real numbers except the zero, because the denominator can not be zero
Multiply by
![[3x(x+4)7x]](https://img.qammunity.org/2018/formulas/mathematics/high-school/zcqmajpxr7xrqro4ys43x37zgbfc9aqm0c.png) both sides
both sides
![(3[3x(x+4)7x])/(3x)+([3x(x+4)7x])/(x+4)=(10[3x(x+4)7x])/(7x)](https://img.qammunity.org/2018/formulas/mathematics/high-school/vlt0ub4qqbotb2l6b7c6kgnw0egwpl8n3i.png)
![(3[3x(x+4)7x])/(3x)+([3x(x+4)7x])/(x+4)=(10[3x(x+4)7x])/(7x)](https://img.qammunity.org/2018/formulas/mathematics/high-school/vlt0ub4qqbotb2l6b7c6kgnw0egwpl8n3i.png)
![3[(x+4)7x]+[3x(7x)]=10[3x(x+4)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/kc0joggz9fb6g1uyqs4dtlpying1ynevwc.png)
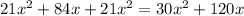
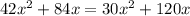
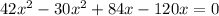
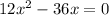
Divide by
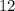 both sides
both sides
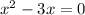
we know that
The formula to solve a quadratic equation of the form
 is equal to
is equal to
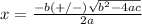
in this problem we have
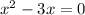
so
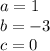
substitute in the formula
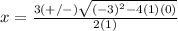
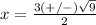
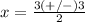
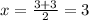
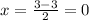
remember that
The domain of the function is all real numbers except the zero
so
the solution is