Answer:
The correct option is 4.
Explanation:
A relation is a function if and only if for each value of x, there exist a unique value of y.
It means if a relation contains
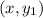 and
and
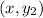 , where
, where
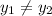 , then the relation is not a function.
, then the relation is not a function.
We need to find a reason why the graph is not a function.
The reason is "it is not a function because there are two different y-values for the single x-value".
Therefore the correct option is 4.