Answer: The correct option is (b) Yes,

Step-by-step explanation: The given sequence is
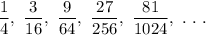
We are to check whether the given sequence is geometric. If so, we are to find the common ration.
GEOMETRIC SEQUENCE: A sequence of numbers where each term is found by multiplying by a constant with the preceding term. This constant is called the common ratio, r.
In the given sequence, we can see
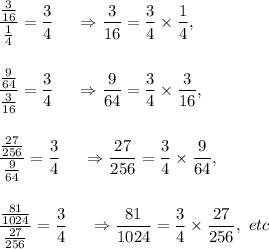
Therefore, each term is found by multiplying
 with the preceding term.
with the preceding term.
Thus, the given sequence is geometric and its common ratio is

Option (b) is correct.